11+ Easiest imo problem info

Home » money laundering idea » 11+ Easiest imo problem info

Your Easiest imo problem images are ready in this website. Easiest imo problem are a topic that is being searched for and liked by netizens today. You can Download the Easiest imo problem files here. Download all royalty-free images.

If you’re looking for easiest imo problem images information related to the easiest imo problem keyword, you have visit the ideal blog. Our website always gives you suggestions for viewing the highest quality video and picture content, please kindly surf and locate more informative video content and images that match your interests.

Easiest Imo Problem. The full IMO problem seems to be in addition to above. To illustrate lets look at the very first problem of the very first IMO Problem 1 of 1959. In particular fp0q 2fpn. Here is a problem on divisibility from the second day of IMO 2018.

Very First Imo Problem In History 1959 Imo Problem 1 The Og Done Three Ways Youtube From youtube.com

Anti money laundering act rbi Anti money laundering act of 2020 beneficial owner Anti money laundering act pdf Anti money laundering act 2017 kenya

Surely It was the legendry Problem 6 IMO 1988. In particular fp0q 2fpn. A sequence of real numbers a0a1a2is defined by the formula ai1 baichaii for i 0. Prove that fx 0 for all x le 0. This combinatorics problem about an anti-Pascal triangle is easy to state but hard to solve. IMO Math MathOlympiadHere is the solution to IMO 1964 Problem 1Subscribe letsthinkcritically.

Number Theory Level 3 d d d is a positive integer not equal to 2 5 2 5 2 5 or 13 13 1 3.

You can view IMO problems on the official IMO website. This problem is considered to be one of the hardest problems ever because none of the members of the strongest teams ie. IMO 2021 Problem 2. This combinatorics problem about an anti-Pascal triangle is easy to state but hard to solve. Some of the easiest problems that came in IMO International Mathematics Olympiad are as follows. This was question 2 on day one of the competition.

Source: quora.com

Prove that fx 0 for all x le 0. Substituting a 1b n gives fpfpn1qq fp2q2fpnq. By design the first problem for each day problems 1 and 4 are meant to be the easiest the second problems. Id like to discuss some of the problems given at this years International Mathematical Olympiad held virtually in St. This problem is considered to be one of the hardest problems ever because none of the members of the strongest teams ie.

Source: pinterest.com

Substituting a 1b n gives fpfpn1qq fp2q2fpnq. In particular fp0q 2fpn. For every integer n prove that the fraction 21 n 4 14 n 3 cannot be reduced any further. Substituting a 0b n1 gives fpfpn1qq fp0q2fpn1q. IMO Math MathOlympiadHere is the solution to IMO 1964 Problem 1Subscribe letsthinkcritically.

Source: medium.com

Videos you watch may. Surely It was the legendry Problem 6 IMO 1988. Let and be positive integers such that divides. You can view IMO problems on the official IMO website. Prove that fx 0 for all x le 0.

Source: youtube.com

If playback doesnt begin shortly try restarting your device. The full IMO problem seems to be in addition to above. About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy Safety How YouTube works Test new features Press Copyright Contact us Creators. THE EASIEST IMO PROBLEM EVER. For every integer n prove that the fraction 21 n 4 14 n 3 cannot be reduced any further.

Source: quora.com

This cannot be the easy part because if you assume f00 then its easy to solve the rest of the problem. Prove that ai ai2 for isufficiently large. Id like to discuss some of the problems given at this years International Mathematical Olympiad held virtually in St. Solved using Euclids algorithm. Substituting a 1b n gives fpfpn1qq fp2q2fpnq.

Source: iq.opengenus.org

An Easy IMO Problem. In particular fp0q 2fpn. Number Theory Level 3 d d d is a positive integer not equal to 2 5 2 5 2 5 or 13 13 1 3. The creator of this problem was Bayarmagnai Gombodorj Team Leader from Mongolia. Videos you watch may.

Source: youtube.com

Nairi Sedrakyan is the author of one of the hardest problems ever proposed in the history of the International Mathematical Olympiad IMO 5th problem of 37th IMO. You can view IMO problems on the official IMO website. Here is a creative solution. Most solutions to this problem first prove that f must be linear before determining all linear functions satisfying 1. To illustrate lets look at the very first problem of the very first IMO Problem 1 of 1959.

Source: youtube.com

A sequence of real numbers a0a1a2is defined by the formula ai1 baichaii for i 0. SOLVED IN ONLY TWO MINUTES. Today this problem seems laughably easy. Number Theory Level 3 d d d is a positive integer not equal to 2 5 2 5 2 5 or 13 13 1 3. Solved using AM GM inequality.

Source: quora.com

By design the first problem for each day problems 1 and 4 are meant to be the easiest the second problems. THE EASIEST IMO PROBLEM EVER. Again the screenshot is taken from the 2018 IMO problem shortlist which also contains the creators suggested solution. IMO 1984 Problem 1. IMO Math MathOlympiadHere is the solution to IMO 1964 Problem 1Subscribe letsthinkcritically.

Source: quora.com

Prove that fx 0 for all x le 0. First note that if a0 0 then all ai 0For ai 1 we have in view of haii. Today this problem seems laughably easy. Let n² be an integer. Substituting a 1b n gives fpfpn1qq fp2q2fpnq.

Source: youtube.com

Surely It was the legendry Problem 6 IMO 1988. To illustrate lets look at the very first problem of the very first IMO Problem 1 of 1959. Substituting a 1b n gives fpfpn1qq fp2q2fpnq. IMO 1959 Problem 1. Today this problem seems laughably easy.

Source: quora.com

63 rows Language versions of problems are not complete. This cannot be the easy part because if you assume f00 then its easy to solve the rest of the problem. The Hardest and Easiest IMO Problems The IMO is a two day contest in which students have 45 hours to solve three problems on each of the two days. Show that must be a perfect square Well Its seeming like a simple problem but it is nothing like that lets get some information about it. By design the first problem for each day problems 1 and 4 are meant to be the easiest the second problems.

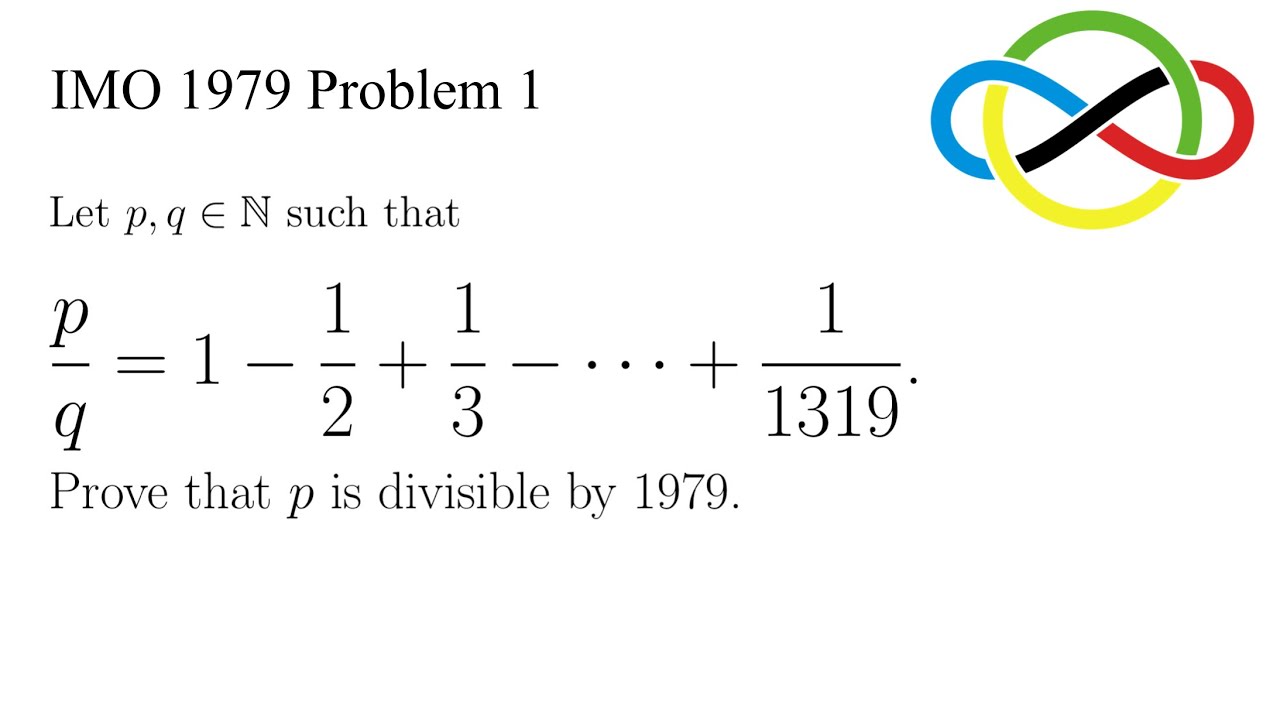Source: youtube.com

63 rows Language versions of problems are not complete. Solved using simple modulus. Solved using Euclids algorithm. Here a0 is an arbitrary real number baic denotes the greatest integer not exceeding ai and haii aibaic. IMO 1984 Problem 1.

This site is an open community for users to do submittion their favorite wallpapers on the internet, all images or pictures in this website are for personal wallpaper use only, it is stricly prohibited to use this wallpaper for commercial purposes, if you are the author and find this image is shared without your permission, please kindly raise a DMCA report to Us.

If you find this site serviceableness, please support us by sharing this posts to your own social media accounts like Facebook, Instagram and so on or you can also bookmark this blog page with the title easiest imo problem by using Ctrl + D for devices a laptop with a Windows operating system or Command + D for laptops with an Apple operating system. If you use a smartphone, you can also use the drawer menu of the browser you are using. Whether it’s a Windows, Mac, iOS or Android operating system, you will still be able to bookmark this website.